
|

|
| Home | Articles | Reviews | Interviews | Glossary | Features | Discussions | Search | Contribute | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Home > Articles > Neural Networks > Beginner
IntroductionIn this article I'll try to explain how you can make a network capable of summing numbers as big as you want. The main thing is that when I ask a person to sum two big numbers he or she can't tell me immediately what is their sum but if I wait enough he can sum them on paper because he or she knows the algorithm. So here we'll try to learn the network the algorithm for summing numbers. We will work with binary numbers because it is easier to make the network for them. I think everyone reading this article can convert decimal numbers to binary and binary to decimal. So when programming you'll have to convert decimal numbers to binary and give them to the neural network and when the network produces a binary number you'll have to convert it to decimal for convinience.AlgorithmThe algorithm for summing two decimal numbers is as follows:
The algorithm for summing binary numbers is almost the same. The difference is that we have only two digits (0 and 1) so the result of summing any two digits can be 0, 1 or 2. Here is a table that illustrates it:
But as we see in step 5 we sum not only the two digits. We add the carry too, which can be 0 or 1 again. Here are all the possible sums of two binary digits and a carry:
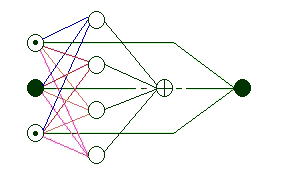
Designing the networkIn all the summing process we have a carry except for the first digits so let's imagine that we have a carry of 0 for them. Our network will sum three binary digits and will produce an output of two binary digits. It will be designed for doing only this but when we learn one such network to produce the right output it can be copied n times and this will result in a network capable of summing numbers as big as 2^n. For example 32 copies of our network will be able to sum numbers as big as 4 000 000 000. So the input of the network will be fed into 3 input neurons - two neurons for the two digits and one neuron for the carry. There will be 2 output neurons - one for the result's last digit and one for the new carry. The neural network will have four neurons in the hidden layer - this I'll explain later. Now you'll probably ask "How should I know the carries? And why do I have to input them to the network". You don't have to. The input and output neurons for the carry you will use only in the learning process. During the summing the learnt networks will be wired up in such manner that each will recieve the carry from the one before it and will give the new carry to the one after it. The network will look like this:
In Figure 1 the white circles are the hidden neurons, the black ones are for the carries, the two with a black dot are inputs for the digits and the one with a plus sign is for the output digit. The green lines come out from the three input neurons and reach the output neuron for the new carry. The middle one is not connected to the output neuron with the plus sign - that's why it is dashed around it. Imagine it as this line is beneath the output neuron. The network is drawn this way for convinience when connecting it to its copies. In the process of learning we will input the network with all the possible sums of three binary digits and we will give it the corresponding correct output of a last digit of the result and a new carry. These sums can be taken from the last colon of Table 2. The most interesting thing in my opinion is
why it works. I'll start with an example - the XOR network. The xor problem is
devided in subproblems. A xor B = (not A and B) or (A and not B). So a network
solving this xor problem would have two hidden neurons - one for solving (not A
and B) and one for (A and not B), and a neuron that gets the outputs of the two
before it and solves the OR problem with them. This makes the XOR network work.
Here we have the same thing. Look at the table bellow, which is actually the
last column of Table 2, with the sums ordered in different way: What we see in Table 3 is that the sums are grouped according the result they give and also we see that in each group there is similarity between the three digits. In the first group there are no 1s. In the second group there is exactly one 1 in every sum. In the third group there are exactly two 1s in each sum. And in the fourth group there are three 1s in the sum. This is the most important part of designing our network because with these rules we will devide our big problem into subproblems. So we start with the output neuron for the new carry (the right black one). We look at Table 3 and we see that it is 1 when there are at least two 1s in the three input neurons, otherwise it is zero - this is solved by the weights of the green lines. The output neuron for the last digit of the result is a little bit harder to be learnt. We look again at Table 3 and we see that it is 1 when all the three input neurons are 1s or exactly one of them is 1, otherwise it is zero. We will devide this more - it is one when (all the inputs are 1s) OR (the first is 1 and the other two are 0) OR
(the second is 1 and the other two are 0) OR (the third is 1 and the other two are
0). The ORs between these subproblems are done by the output neuron itself and the weights of the four black lines. That is why this network works. And that is why it has four hidden neurons. I suggest you learn it using the back propagation algorithm. I will not explain it in this article, but there are many words written about it and how it works.
Wiring upHere we'll see how the learnt networks are wired up in a row one to another. So we learn one network of the type that is shown above and we decide that we want our AI program to be able of summing numbers as big as 2^n. We make this much copies of the network. We know that one network can sum one bit of each of the two numbers and a carry so we must wire 2^n learnt networks for each bit and another for a possible new bit. The wiring of the networks will look like this:
This structure will be able of summing one bit numbers only. If we want it to sum the numbers 1 and 0 we input the left one with these numbers and a carry of 0. We run the networks and the output neurons (the ones with a plus sign) will produce 01 (right to left). In other words we put the bits of the first number to be summed in the upper input neurons (the rightmost bit is the first to be put), we put the bits of the second number in the lower input neurons of the networks (the rightmost bit is the first to be put), we put zeros in the two input neurons of the last (n+1)th network (this does not change the numbers) and we input the first network's carry input neuron with a zero, because there is no carry in the beginning. Then we run each network individually, left to right, and we round the results in the two output neurons so that the whole network is more accurate. Then we have the result of the summing in the output neurons (with the plus sign) of each network representing the bits of the number. The leftmost output is the rightmost bit of the result. This structure works because each network recieves two digits and a carry to be summed and it produces the digit to be written down and the new carry which is directly given to the next network.
ConclusionIn conclusion I wish to say that this is not a network that learns the algorithm as a human. It learns only the main sums for binary summing. The algorithm comes when you wire up the networks. The interesting is how to make a network capable of learning the algorithm itself.Summing Demonstration ProgramAyrun submitted a demonstration program using C++/MFC that graphical helps illustrate the concepts in this article.
Submitted: 27/08/2003 Article content copyright © Stephen Tashev, 2003.
|
|






 Figure
1
Figure
1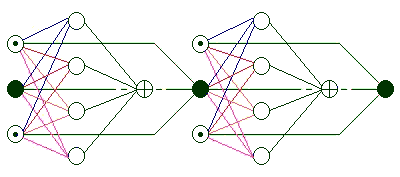 Figure
2
Figure
2
 Print
Print E-mail description
E-mail description BibTeX entry
BibTeX entry